目录：

1️⃣ 环境：一种管理变量的数据结构 ​

🚀 环境是ECMAScript规范中用于管理变量的一种数据结构

• 它是一个字典，其keys是变量名，其值是对应变量的值
• 每个作用域（scope）都有相关联的环境
• 💡环境必须支持以下与变量相关的现象
  • 递归（Recursion）
  • 嵌套作用域（Nested scopes）
  • 闭包（Closures）

接下来会用示例演示每一种现象是如何完成的。

2️⃣ 通过环境进行递归 ​

我们先处理递归，演示代码：

function f(x) {
  return x * 2
}

function g(y) {
  const tmp = y + 1
  return f(tmp)
}

assert.equal(g(3), 8)

对每个函数的调用，你需要为调用的函数的变量（参数和本地变量）刷新存储空间。

👩🏻‍🏫

1. 这是通过一种叫做 执行上下文（execution contexts）的栈管理的，这个执行上下文指向环境（environments）😎
2. 环境自身是存在于堆（Heap）中的。存在于堆中是有必要的，因为在执行离开它们的作用域后，它们偶尔会继续存在（闭包现象）。因此它们不能通过栈就行管理

2.1 执行代码 ​

当执行代码时，我们做下面暂停⏸（pauses）:

function f(x) {
  // 暂停3
  return x * 2
}

function g(y) {
  const tmp = y + 1
  // 暂停2
  return f(tmp)
}

// 暂停1
assert.equal(g(3), 8)

这个过程是：

• 暂停1：在调用 g() 之前
• 暂停2：当执行 g() 时
• 暂停3：当执行 f() 时
• 剩下步骤：每次碰到 return 语句时，一个 执行上下文（execution context） 从栈（stack） 中移除

步骤图解：

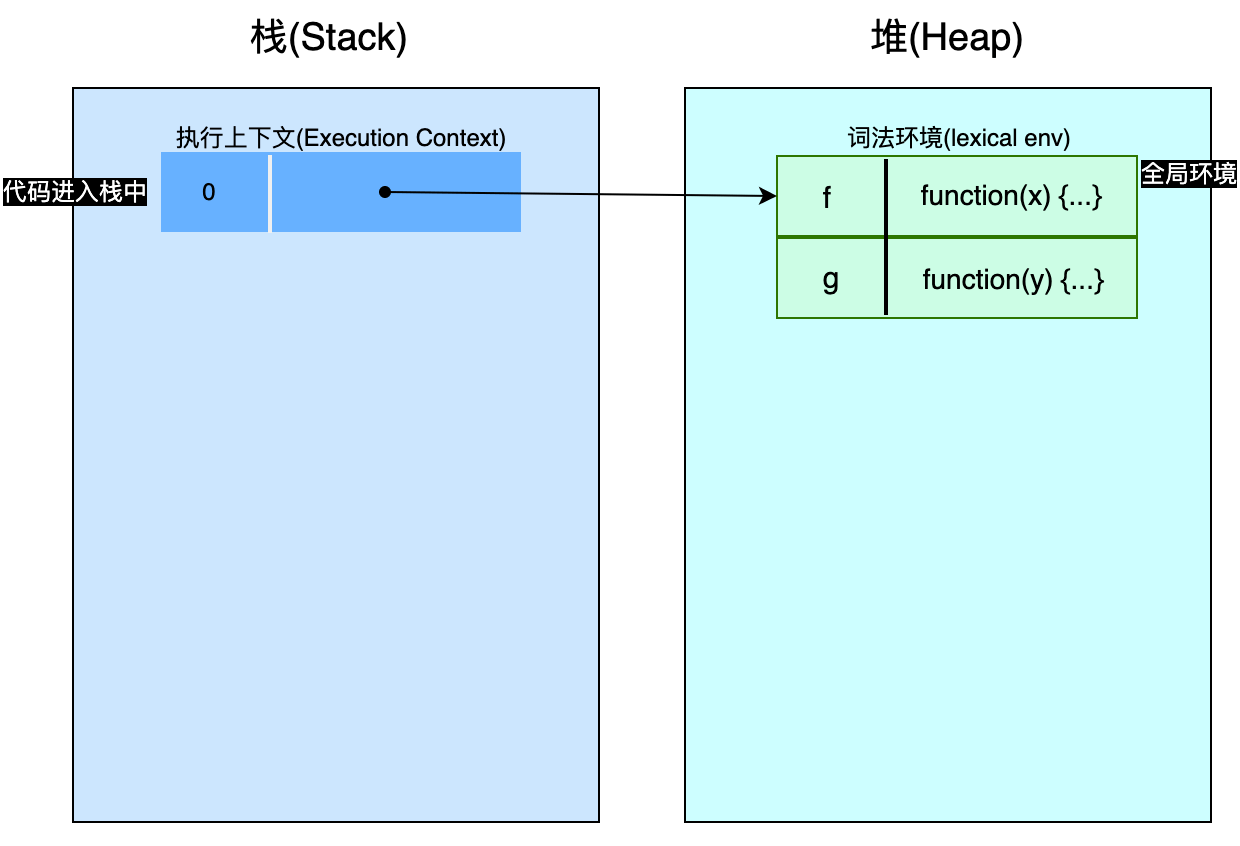
👆🏻暂停1 - 在调用 g() 之前：执行上下文栈有一个条目(entry)，指向最顶层的环境（译者注：最顶层环境为全局环境）。在这个环境中有2个条目：一个是f()另一个是 g()。

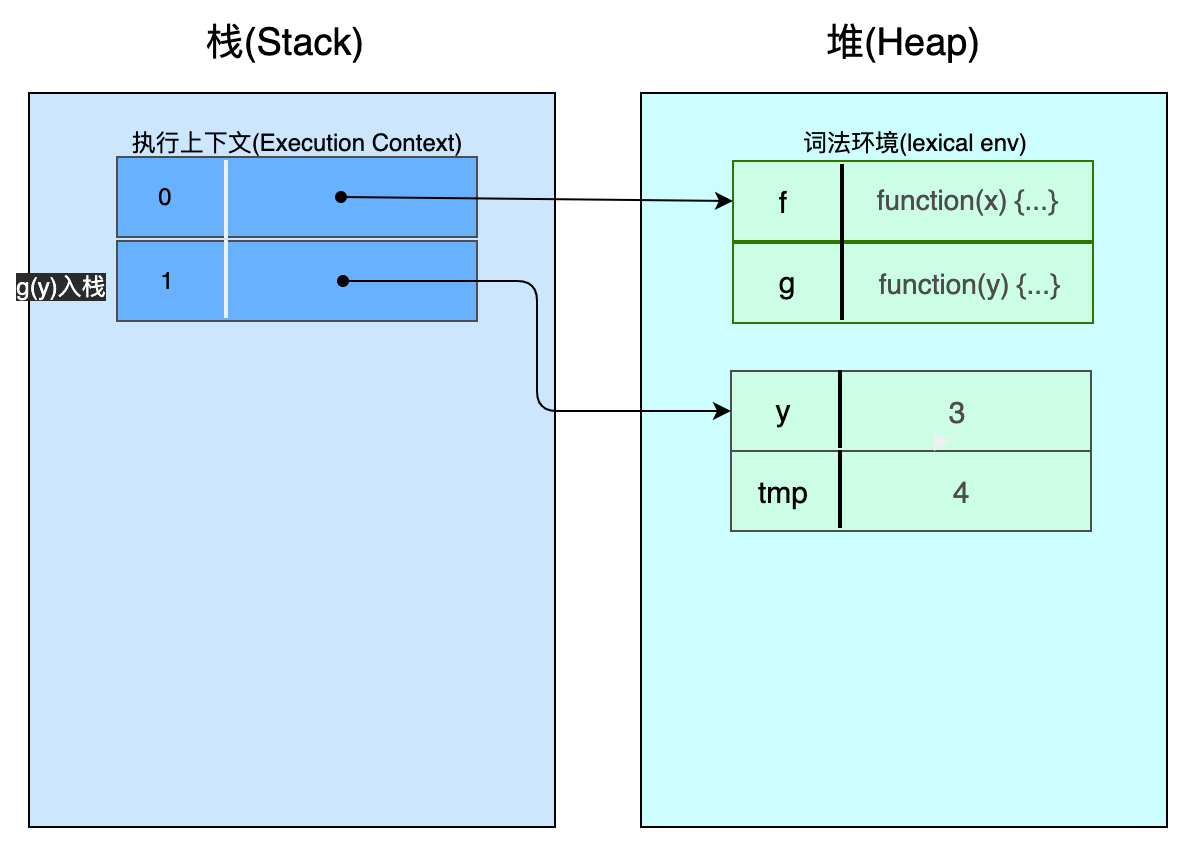
暂停2 - 执行 g() 时：最顶部的执行上下文栈（译者注：调用g()函数时，g()函数压入栈，位于栈的最顶部）指向为 g() 函数创建的环境（新的一个环境）。这个环境包括了参数 y 和本地变量 tmp 2个条目。

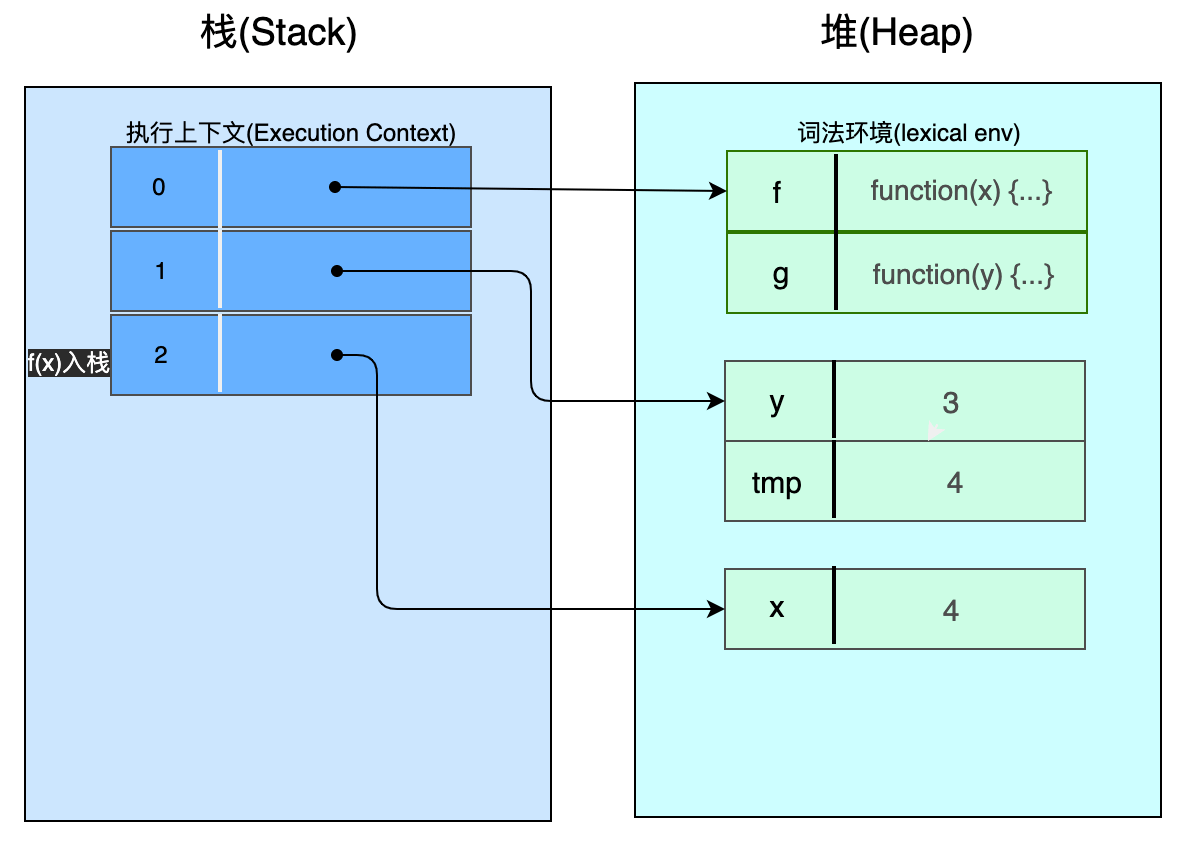
暂停3 - 当执行 f() 函数时：最上层的执行上下文（译者注：此时是 f(x) 在栈的最上层）指向 f() 创建的环境。

3️⃣ 通过环境形成嵌套作用域 ​

使用下面代码探索如何通过环境形成嵌套作用域（Nestes Scopes）:

function f(x) {
  function square() {
    const result = x * x
    return result
  }
  
  return sqaure()
}

assert.equal(f(6), 36)

这里我们有3个嵌套作用域：最上层的作用域（译者注：全局作用域），f() 的作用域，square() 的作用域。观察：

• 📚作用域是连在一起的。内部作用域继承所有外部作用域的变量，除了哪些被遮挡（shadowed）的变量（译者注：比如外部作用域定义了一个 const a = 10, 而内部作用域也定义了一个 a 变量，则内部作用域的变量 a 会遮挡外部作用域的变量 a）
• 嵌套作用域是独立于递归的机制。递归最好由独立的环境堆管理，而嵌套作用域则表示环境与其创建环境之间的关系

🚀 因此，每个作用域的环境通过一个名为 outer 的属性指向它周围作用域的环境。

• 当我们查询一个变量的值时，我们先在当前环境中搜索该名字的变量
• 如果找不到就在其外部环境（outer environment）中查找，如果还找不到，就接着在外部环境的外部环境中查找（译者注：类似原型链）
• 当前环境能访问整个外部环境链中包含的所有变量（除了遮挡的变量）

🚀 当你调用函数时，就会创建一个新的环境。当前环境的外部环境是创建该函数的环境📚。为了帮助设置通过函数调用而生成的环境的 outer 属性，每个函数内部有一个叫 [[Scope]] 的属性会指向其出生环境（birth environment） 🤩。

3.1 执行代码 ​

下面是我们执行代码是的暂停点：

function f(x) {
  function square() {
    const result = x * x
    // 暂停3
    return result
  }
  
  // 暂停2
  return sqaure()
}

// 暂停1
assert.equal(f(6), 36)

这个过程是：

• 暂停1 - 在调用 f() 函数前
• 暂停2 - 当执行 f() 函数时
• 暂停3 - 当执行 square() 函数时
• 之后，return 语句函数出栈

步骤图解：

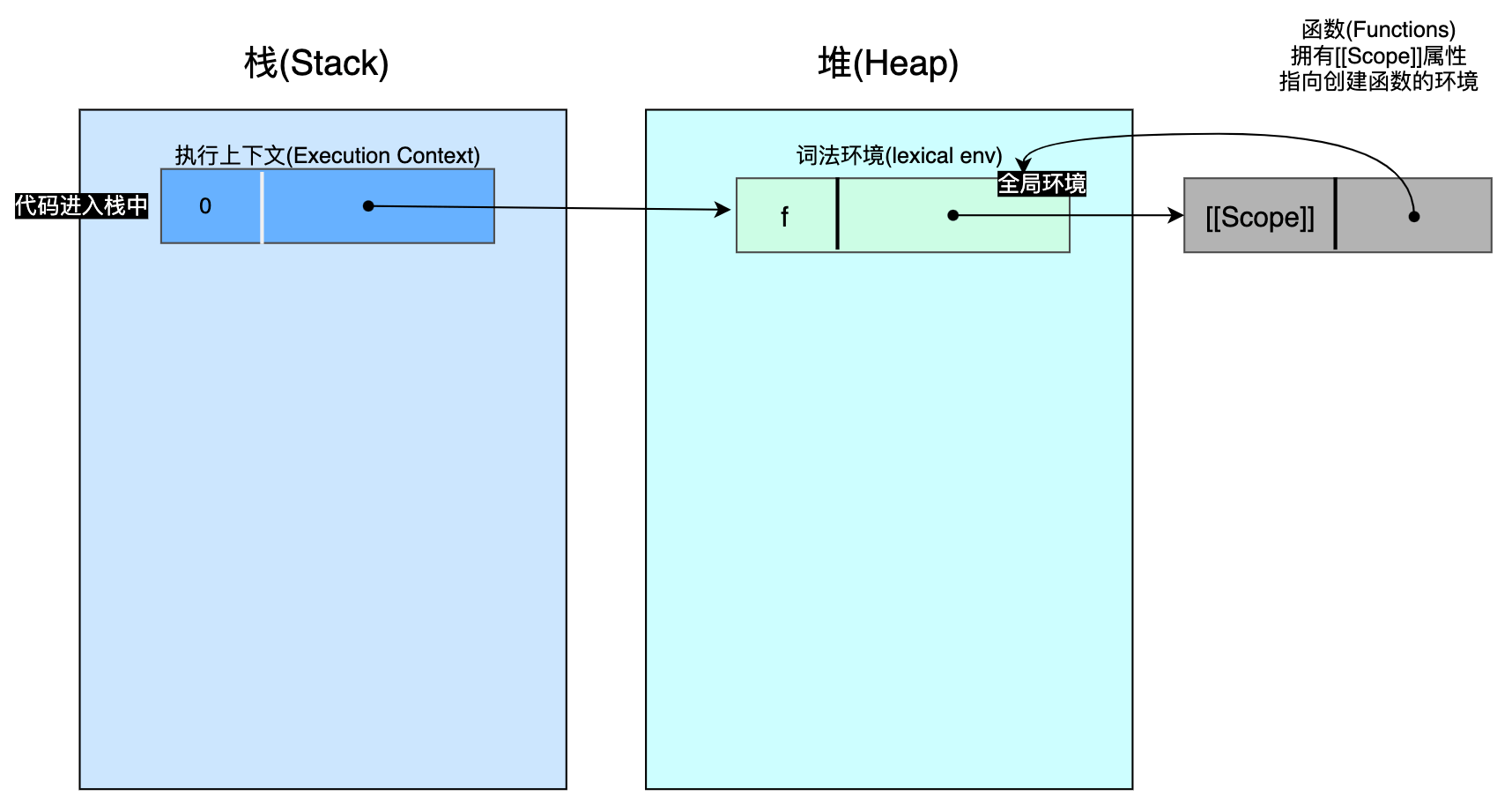
👆🏻暂停1 - 在调用 f() 函数前：最上层环境（全局环境）有一个条目，即 f()。 而 f() 函数的出生环境为最上层环境（译者注：即这里的全局环境）。因此 f 函数的 [[Scope]] 指向这个全局环境。

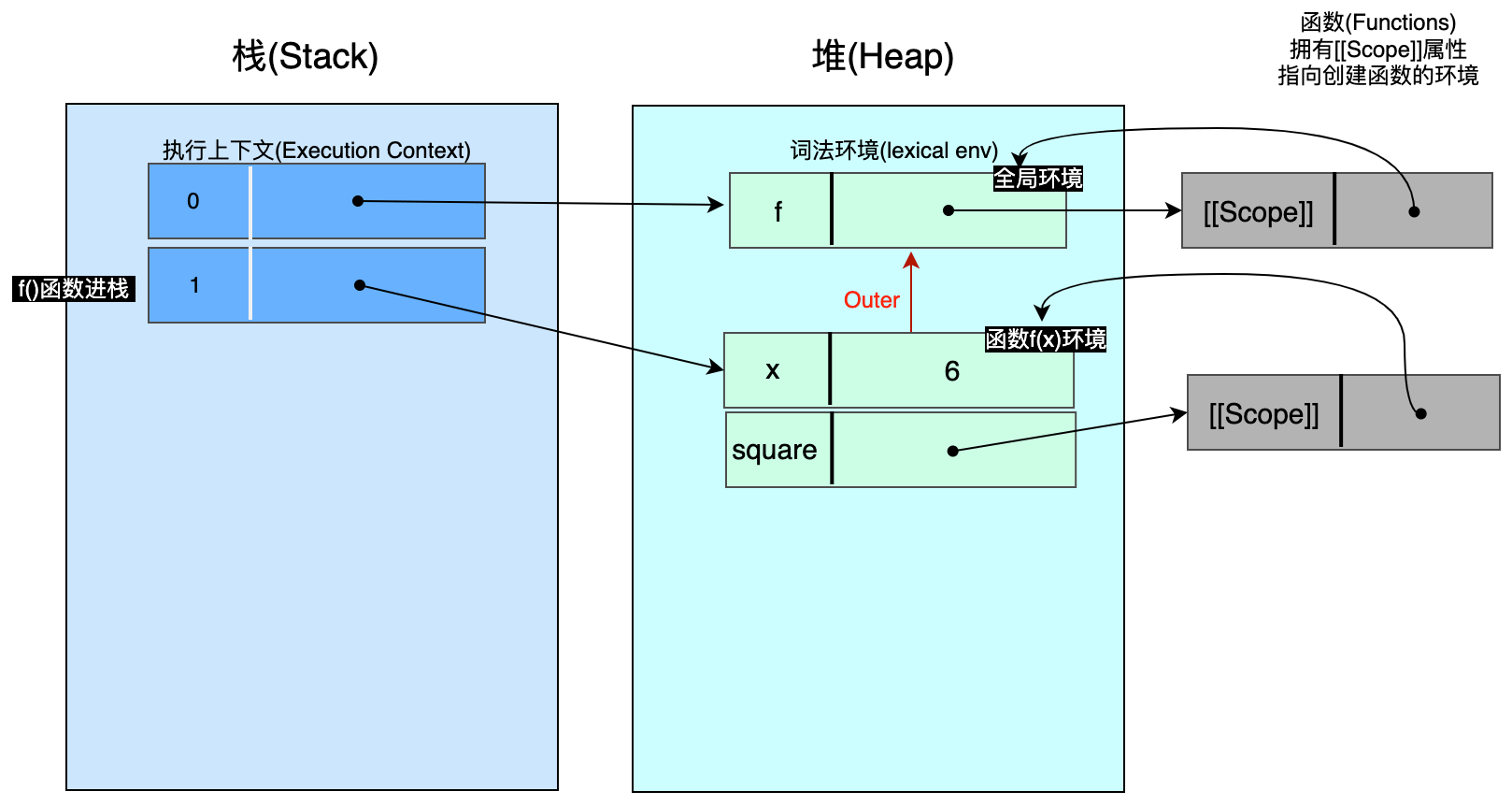
暂停2 - 当执行 f() 函数时：现在已经存在一个调用 f(6) 的环境了（译者注：全局环境）。全局环境是f() 函数执行时所生成的环境的出生环境，因此执行 f() 函数的环境的 outer 属性指向全局环境。而新函数 square() 的 [[Scope]] 指向创建它的环境（即这里的 f(x)执行生成的环境）。

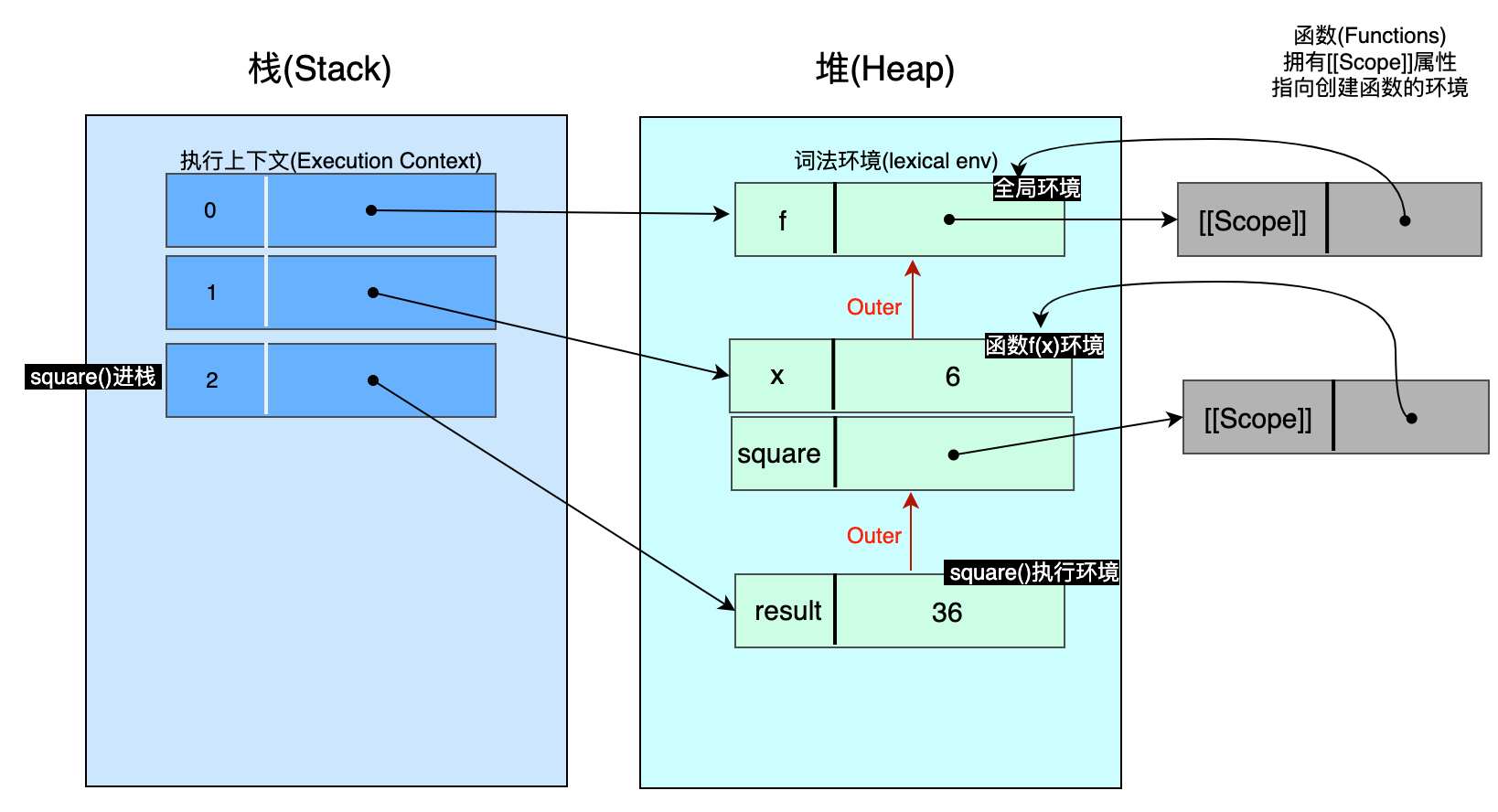
暂停3 - 当执行 square() 函数时：重复先前模式：square函数执行生成的环境的 outer 指向其 [[Scope]] 指向的环境。作用域链通过 outer 属性创建，包含所有活动的变量📚。例如，如果我们愿意的话，可以访问 result & square & f 变量。环境反应了变量的2个方面：

1. 外部环境链反应了嵌套静态作用域
2. 执行上下文栈反应了正在动态调用哪一个函数

4️⃣ 闭包与环境 ​

为了了解环境如何用于实现 闭包（closures），我们使用下面示例：

function add(x) {
  return (y) => { // A
    return x + y
  }
}

assert.equal(add(3)(1), 4) // B

这里发生了什么？add() 是一个函数，它返回另一个函数。当我们在B行位置调用嵌套函数 add(3)(1) 时，第一个参数是给 add() 的，第2个参数则是给它返回的函数的。 这是可行的，因为在A行位置创建的函数在离开出生作用域（birth scope）时不会失去与该作用域的连接。 关联的环境通过这种联系得以存活下来，函数仍可访问变量 那个环境中的 x（x在该函数中被释放）。

这种嵌套调用 add() 的方式有个优点：你可以先调用第一个函数，得到一个参数已经填充的 add() 版本：

const plus2 = add(2)
assert(plus2(5), 7)

📚将一个有2个参数的函数转换为参数各1个的2个嵌套的函数，这称之为库里（currying）, add() 就是一个库里化的函数。

只填充函数的部分参数称之为 部分应用（partial application） （函数还没有完全应用）。bind() 函数便执行了部分应用。在上面的例子中，我们可以发现，对一个函数进行库里化，部分应用变得很简单。

4.1 执行代码 ​

当我们执行上面代码时，添加3个暂停点：

function add(x) {
  return y => {
    // 暂停3：plus2(5)
    return x + y
  } // 暂停1：add(2)
}

const plus2 = add(2)

// 暂停2
assert.equal(plus2(5), 7)

这个过程是：

• 暂停1 - 在执行 add(2) 过程
• 暂停2 - 在执行 add(2) 之后
• 暂停3 - 当执行 plus2(5) 时

步骤图解：

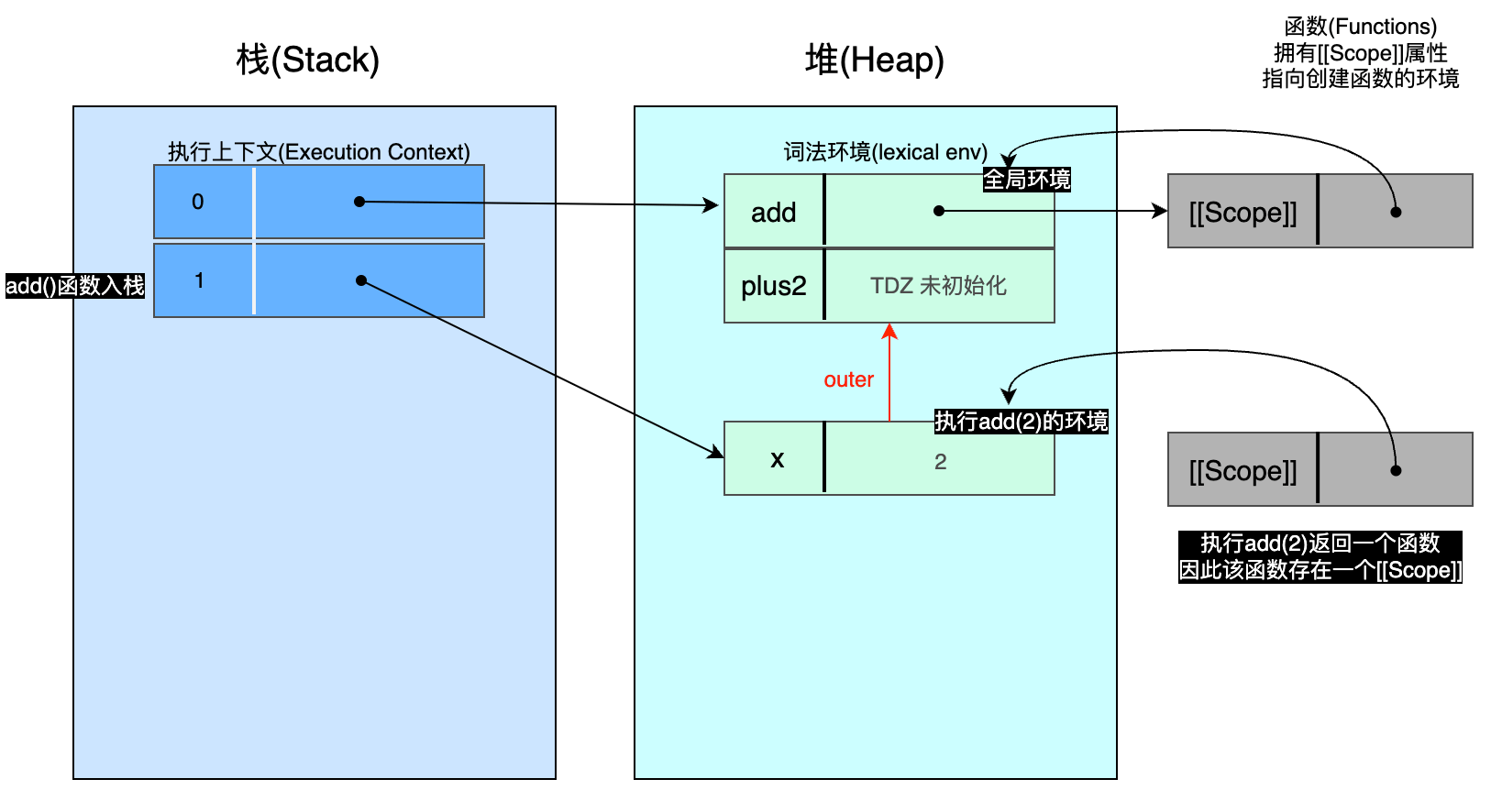
👆🏻暂停1 - 在执行 add(2) 过程：这里可以看到 add() 返回的函数已经存在（右下角），因此返回的函数的内部属性 [[Scope]] 指向它的出生环境（birth environment）。

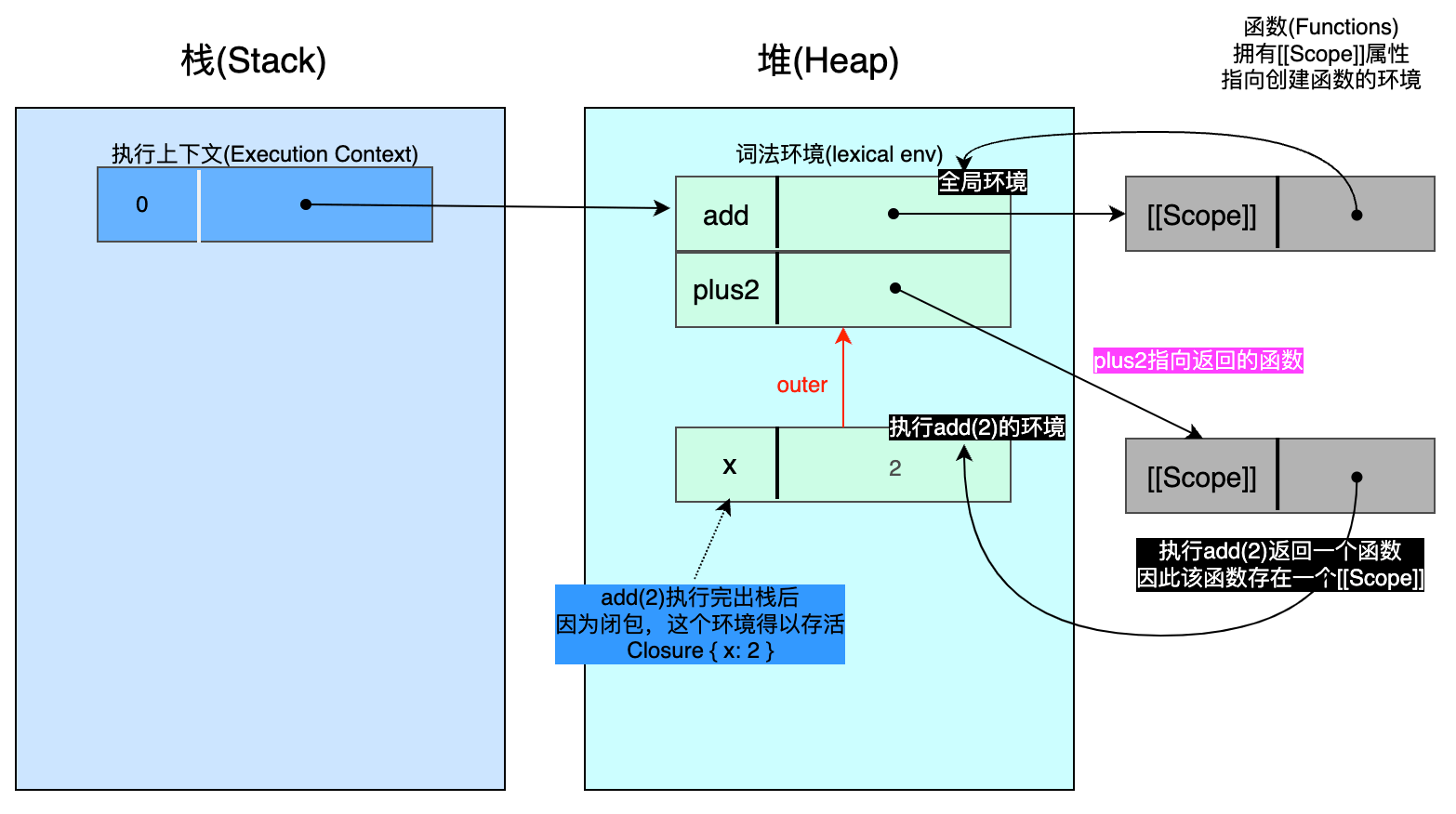
🚀暂停2 - 在执行 add(2) 之后：plus2 现在指向 add(2) 返回的函数。该函数通过 [[Scope]] 属性保持它的出生环境（即 add(2) 执行环境）在 add(2) 执行完成出栈之后仍旧存活。

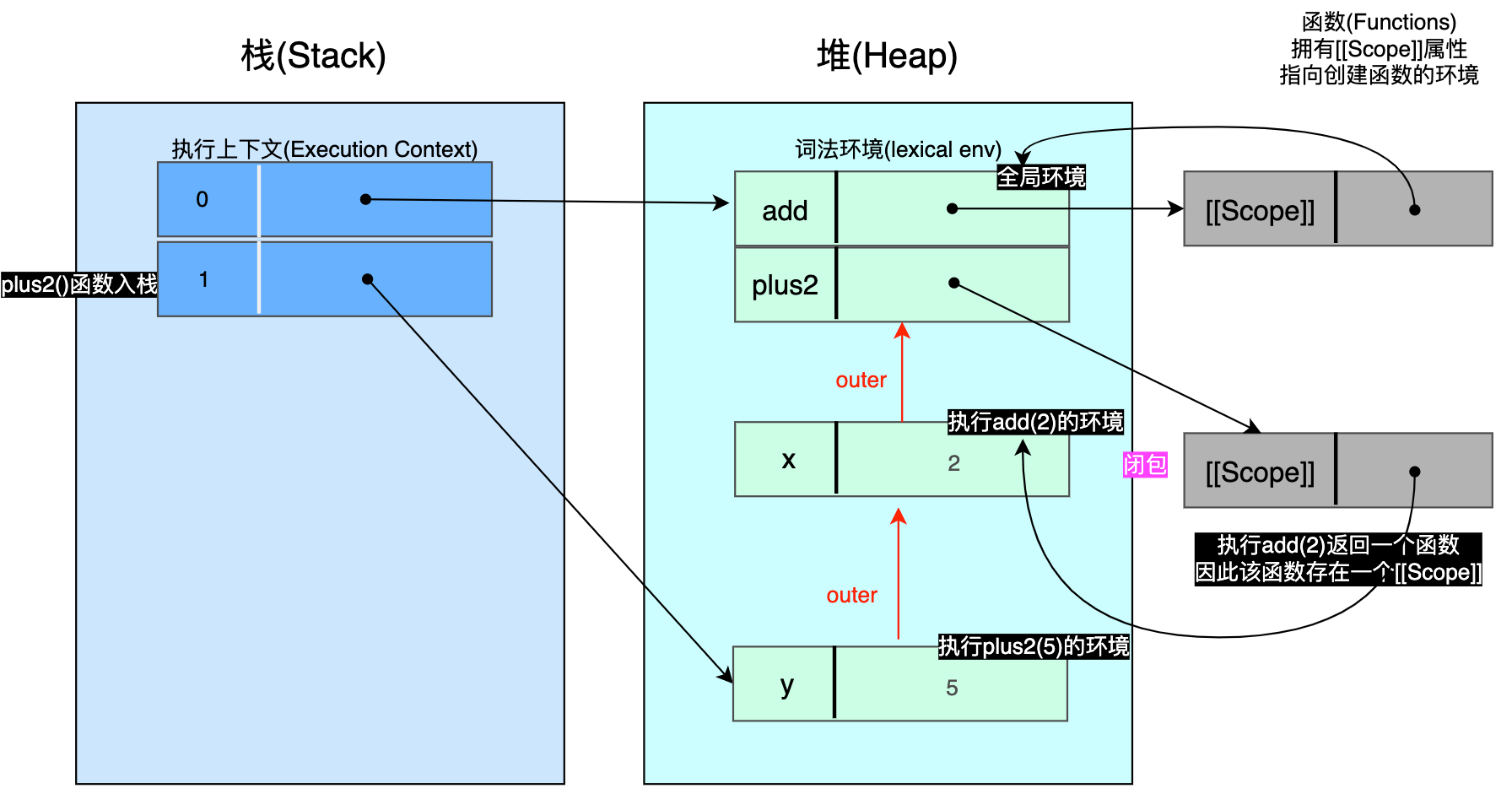
暂停3 - 当执行 plus2(5) 时：执行 plus2(5) 产生的新环境的 outer属性指向 plus2 指向的 [[Scope]] 指向的环境，这也是为什么当前函数能访问 x 的原因 😎。

原文链接：

• 4 Environments: under the hood of variables

2022年07月05日01:04:21

PS: 相比于原版配图，自己画的图添加了一些色彩和注解，但整体流程是一致的。